
Polynomials are one of the most important chapters in the world of maths. When kids are interested in solving different questions, they have to learn multiple formulas. One concept is the remainder theorem which students have to learn in order to solve mathematical problems. Therefore, it’s important that its concept would be clear to the students to understand and solve questions easily.
Here is a guide about the remainder theorem, its definition, proofs, and examples. Check it out:
Remainder Theorem
Finding the reminder with the remainder theorem formula: (px) would be any polynomial of a degree greater than, or equal to one, and can be any real number. If the polynomial (px) is divided by (x – k), then the remainder obtained is (pc). Now that you know what the remainder theorem is, let’s learn about it a bit more.
Remainder Theorem Proof
When we divide (px) simply by the polynomial (x – k ), we get:
![]()
As (x – k) has the degree 1, r (x), is a reminder as well, and it must have a degree of 0.
Therefore, the remainder is just constant r. Accordingly, we’ll get:
![]()
If we substitute x with k, we’ll get:
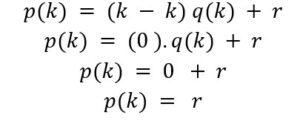
Why The Remainder Is constant in the Remainder Theorem?
The remainder theorem proves states that when the given polynomial gets divided by (x – k) the remainder obtained will either be 0 or a degree less than (x – k). As (x – k) is equal to degree 1, the degree of the remainder must be 0. This implies that the remainder is constant.
Therefore, in either case p(x) = (x – k) q(x) + r(x). In this case, the remainder r is a real number, probably 0. Substituting the variable “x” with ‘k’, we get p(k) = r as required. You can visit Cuemath to learn about this topic in detail.
The Steps to divide the polynomial by the non-zero polynomial are:
- First of all, students need to arrange the polynomials in the decreasing order of degree.
- Then they need to divide the first term of the dividend by the first term of the divisor to produce the first term of the quotient.
- Then one needs to multiply the divisor by the first term of the quotient and subtract this product from the dividend to get the reminder.
- The reminder is the dividend now, and the divisor will remain the same.
- The students would need to repeat this until the degree of the new dividend is less than the degree of divisor.
Remainder Theorem Example
What will be the remainder when the given polynomial:
![]()
Gets divided by x – 1? The solution is:
Let the dividend be
![]()
Let divisor be x – 1
If we equate the divisor to 0, we get: x – 1 = 0 and x = 1.
Therefore, substituting the value of x in the polynomial –
![]() We get:
We get:
![]()
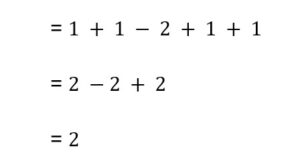
Therefore, the remainder is 2.
Final Words
The popularity of online platforms has increased in recent times as they provide learning facilities for students that are quite beneficial. Various learning management programs are coming up with their online classes to help students continue with their studies with the flexibility of time and location. Students can access online classes from home or anywhere through a secured internet connection. Cuemath is one such learning platform that conducts online classes for mathematics taken by expert teachers who guide students to learn the basic concepts of mathematics. The classes and curriculum are structured in such a way that students of any standard can gain a clear conception of the topics covered in their respective courses. It not only guides students to develop their problem-solving skills but also focuses on building a strong foundation in mathematics.
Cuemath online classes help students to learn some simple yet effective techniques of handling mathematical problems while developing their analytical and reasoning skills. The effective interaction between teachers and students in the online classes helps to bring clarity on the concepts by resolving any doubts on the topics.
Cuemath classes use various application-based tools and innovative methodologies to make the learning enjoyable and avoid the fear of mathematics for the students from an early age. The students are trained in practice-based learning through the solving of various assignments. They can track their progress from the results that help to build their confidence and at the same time highlight the areas of improvement that are taken care of by the teachers. The classes and teaching pedagogy are designed to create a student-friendly environment that increases engagement and facilitates effective learning. Visit the Cuemath website for more information and enroll in a session.
